Integration2See
Die Integration ist ein wichtiges Instrument der Statistik und der Mathematik im Allgemeinen. Veranschaulicht kann mit der Integration die Fläche zwischen einem Funktionsgraphen und der $x$-Achse berechnet werden. Mathematisch betrachtet bildet die Integration das Gegenstück zur Differentiation.
Betrachten wir beispielsweise die Funktion $f \colon \mathbb R \to \mathbb R$ gegeben durch $f(x) := (x-1)^2 + 1$. Der zugehörige Funktionsgraph ist im folgenden Bild im Bereich $[-2, 2]$ dargestellt:
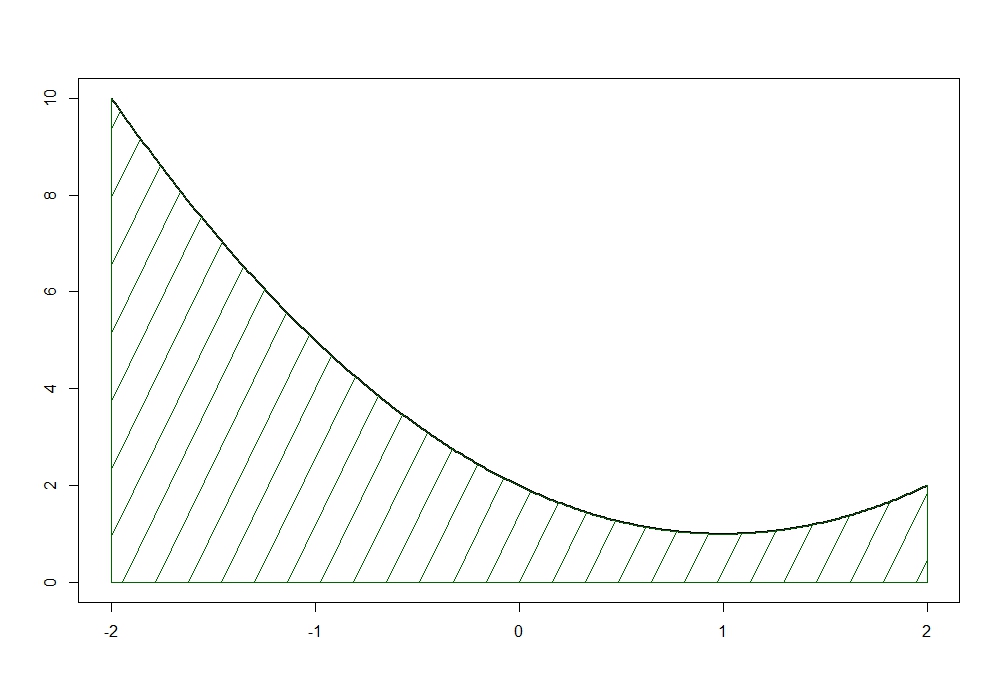
Wir möchten die grün schraffierte Fläche zwischen dem Graphen und der $x$-Achse berechnen.
Wie wird dieser sogenannte Integralwert im Bereich $[-2, 2]$ berechnet? Und wie kann dies veranschaulicht werden? Zunächst wird das bestimmte Integral von $f$ im Intervall $[-2, 2]$ durch
$$\int_{-2}^2 \! f(x) \, \mathrm d x$$
notiert. Hierbei kann statt $x$ auch eine andere Integrationsvariable verwendet werden, beispielweise $t$, also $\int_{-2}^2 \! f(t) \, \mathrm d t$.
Wir wissen bereits, wie man die Fläche einfacher geometrischer Objekte berechnet, beispielsweise eines Rechtecks ("Länge mal Breite") oder eines Kreises ($2 \pi \cdot \text{Radius}^2$). Wir werden nun das Problem der Flächenberechnung zwischen der $x$-Achse und dem Graphen von $f$ auf solch bekannte Formeln zurückzuführen: Hierzu legen wir Rechtecke von gleicher Breite $h$ von unten an den Funktionsgraphen an:
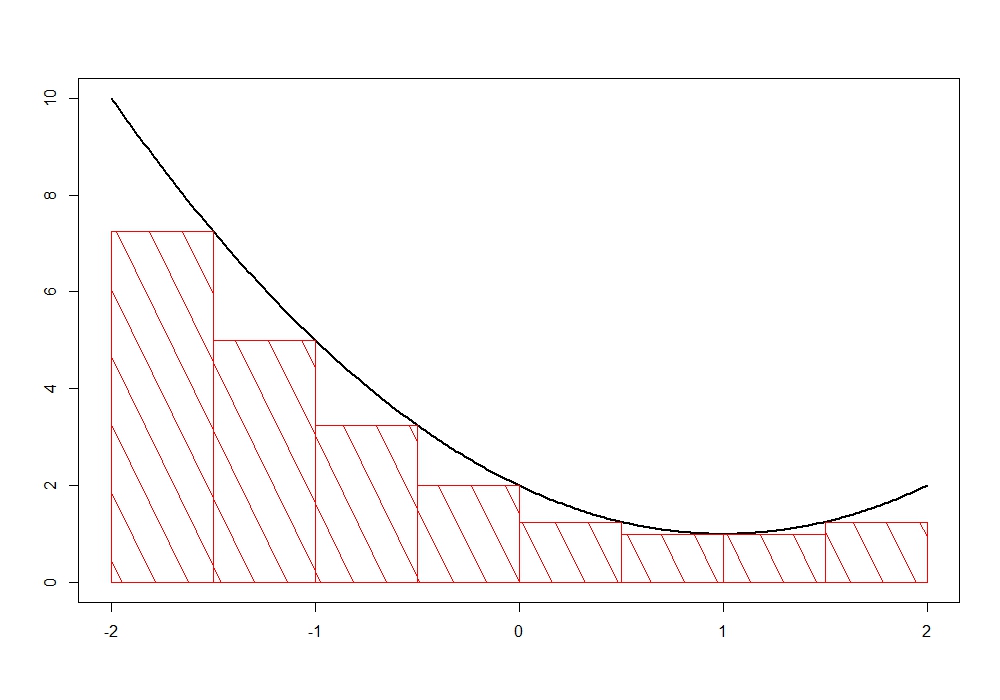
Jedes solche Rechteck wird also über einem Intervall der Form $[t, t+h]$ mit $t \in \{-2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5\}$ eingezeichnet. Hierbei ist $h=0.5$ und die Höhe eines Rechtecks ist gegeben durch $\text{inf}\{f(x) \mid t\leq x \leq t+h\}$. Die Summe der Rechtecksflächen kann somit leicht berechnet werden und heißt Untersumme. Diese ist jedoch etwas kleiner als die gesuchte Fläche.
Wir berechnen nun die Untersumme für dieses Beispiel:
Breite der Rechtecke: jeweils $h=0.5$
Höhen der Rechtecke: $7.25, 5.00, 3.25, 2.00, 1.25, 1.00, 1.00, 1.25$
Flächen der Rechtecke: $3.625, 2.500, 1.625, 1.000, 0.625, 0.500, 0.500, 0.625$
Untersumme: $11$
Analog betrachten wir nun Rechtecke, die etwas größer sind als der Funktionsgraph:
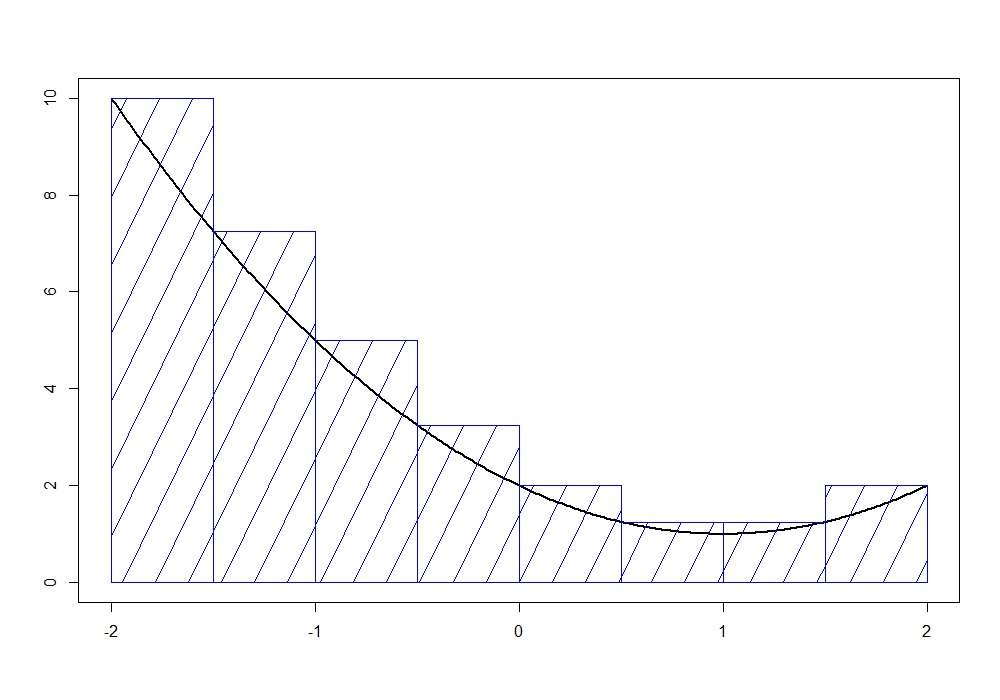
Wie bei der Untersumme, wird auch hier ein Rechteck über ein Intervall der Form$[t, t+h]$ mit $t \in \{-2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5\}$ eingezeichnet. Die Höhe eines Rechtecks ist nun gegeben durch $\text{sup}\{f(x) \mid t\leq x \leq t+h\}$ und die Summe der Rechtecksflächen heißt Obersumme. Diese ist etwas größer als die gesuchte Fläche unter dem Funktionsgraphen.
Wir berechnen nun die Obersumme für dieses Beispiel:
Breite der Rechtecke: jeweils $h=0.5$
Höhen der Rechtecke: $10.00, 7.25, 5.00, 3.25, 2.00, 1.25, 1.25, 2.00$
Flächen der Rechtecke: $5.000, 3.625, 2.500, 1.625, 1.000, 0.625, 0.625, 1.000$
Obersumme: $16$
Der gesuchte Flächeninhalt liegt zwischen der Ober- und der Untersumme, also zwischen $11$ und $16$. Diese Beobachtung nutzen wir nun und wiederholen den Vorgang mit Ober- und Untersumme, aber nun für eine kleinere Breite $h=0.2$. Für Unter- und Obersumme erhalten wir folgende Bilder:
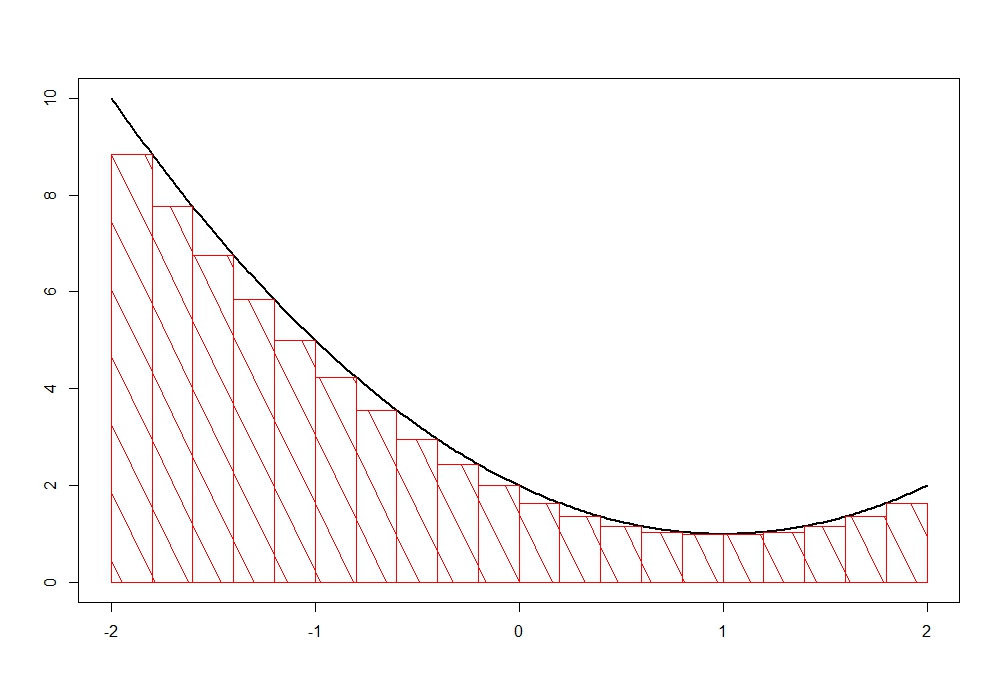
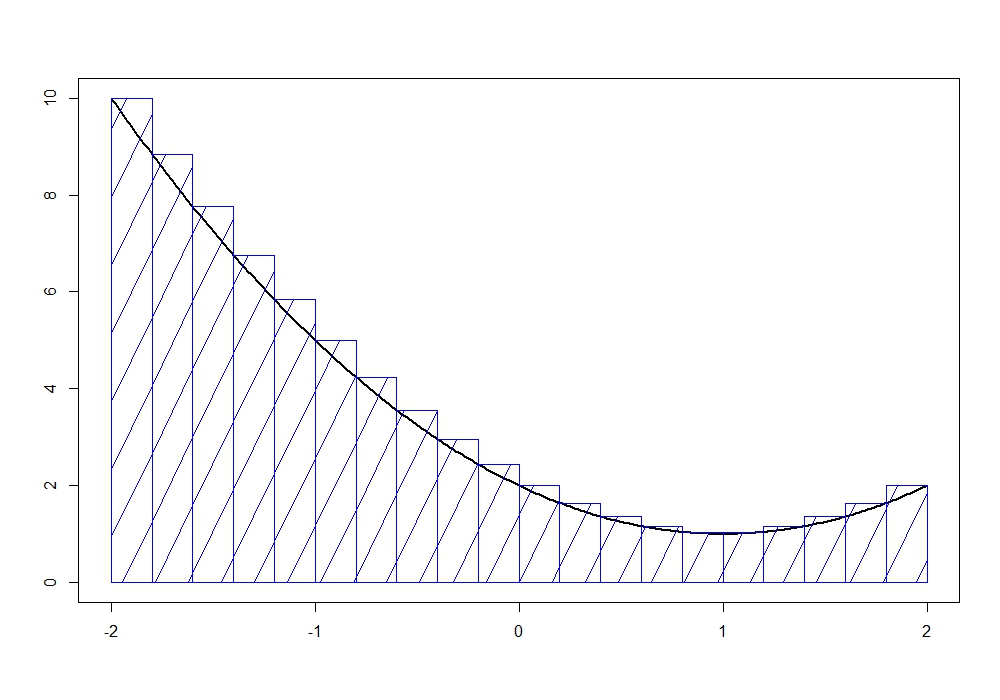
Für $h=0.2$ ergibt sich eine Untersumme von $12.36$ und eine Obersumme von $14.36$. Somit haben wir eine kleinere Spanne für den gesuchten Flächeninhalt gefunden.
Dieses Vorgehen kann nun beliebig oft fortgesetzt und somit eine belibig kleine Spanne, also das Intervall zwischen Unter- und Obersumme, für den Flächeninhalt erreicht werden. Falls es eine Zahl $A\in\mathbb R$ gibt, die für alle Breiten $h>0$ in jedem solchen Intervall liegt, so ist $A$ gerade die gesuchte Fläche! In diesem Fall heißt die Funktion $f$ integrierbar über dem Intervall $[-2,2]$.
Der Integralwert kann mit den bekannten Rechenregeln wie folgt berechnet werden:
\begin{align}\int_{-2}^2 \! f(x) \, \mathrm d x &= \int_{-2}^2 \! (x-1)^2 + 1 \, \mathrm d x\\&= \int_{-2}^2 \! x^2 - 2x + 2 \, \mathrm d x\\&= \left( \frac{x^3}{3} - x^2 + 2x\right)\Bigg|_{-2}^2\\&= \frac{8}{3} - 4 + 4 - \left( -\frac{8}{3} -4 -4\right)\\&=13+\frac{1}{3}\end{align}
Wir sehen, dass der gesuchte Flächeninhalt von $13+\frac{1}{3}$ in beiden Fällen zwischen Unter- und Obersumme liegt!