Vektoren2see

Vektoren sind Objekte, die einen oder mehrere Werte enthalten können. Ein Vektor enthält nur eine Spalte von Werten, z.B.   $\begin{pmatrix}5 \end{pmatrix} $  oder  $\begin{pmatrix}5 \\ 5 \\ 5\end{pmatrix}$.

Multiplikation des Vektors mit einem Skalar
Die Multiplikation eines Vektors mit einem positiven Skalar $\lambda$ ändert nur die Länge des Vektors und nicht die Richtung. Bei der Multiplikation mit einem negativen Skalar ändert sich auch die Richtung des Vektors.
$$
\lambda \cdot \vec{v} \,\,\,=\,\,\, \begin{pmatrix}
\lambda \cdot v_1 \\ \lambda \cdot v_2 \\ \vdots \\\lambda \cdot v_n
\end{pmatrix}
$$

Addition/Subtraktion von Vektoren
Die Addition und Subtraktion von Vektoren erfolgt komponentenweise.
$$
\vec{v} \pm \vec{w} \,\,\,=\,\,\, \begin{pmatrix}
v_1 \\ v_2 \\ \ddots \\v_n
\end{pmatrix} \pm \begin{pmatrix}
w_1 \\ w_2 \\ \ddots \\ w_n
\end{pmatrix}
\,\,\,= \,\,\,
\begin{pmatrix}
v_n \pm w_1 \\ v_n \pm w_2 \\ \ddots \\v_n \pm w_n
\end{pmatrix}
$$

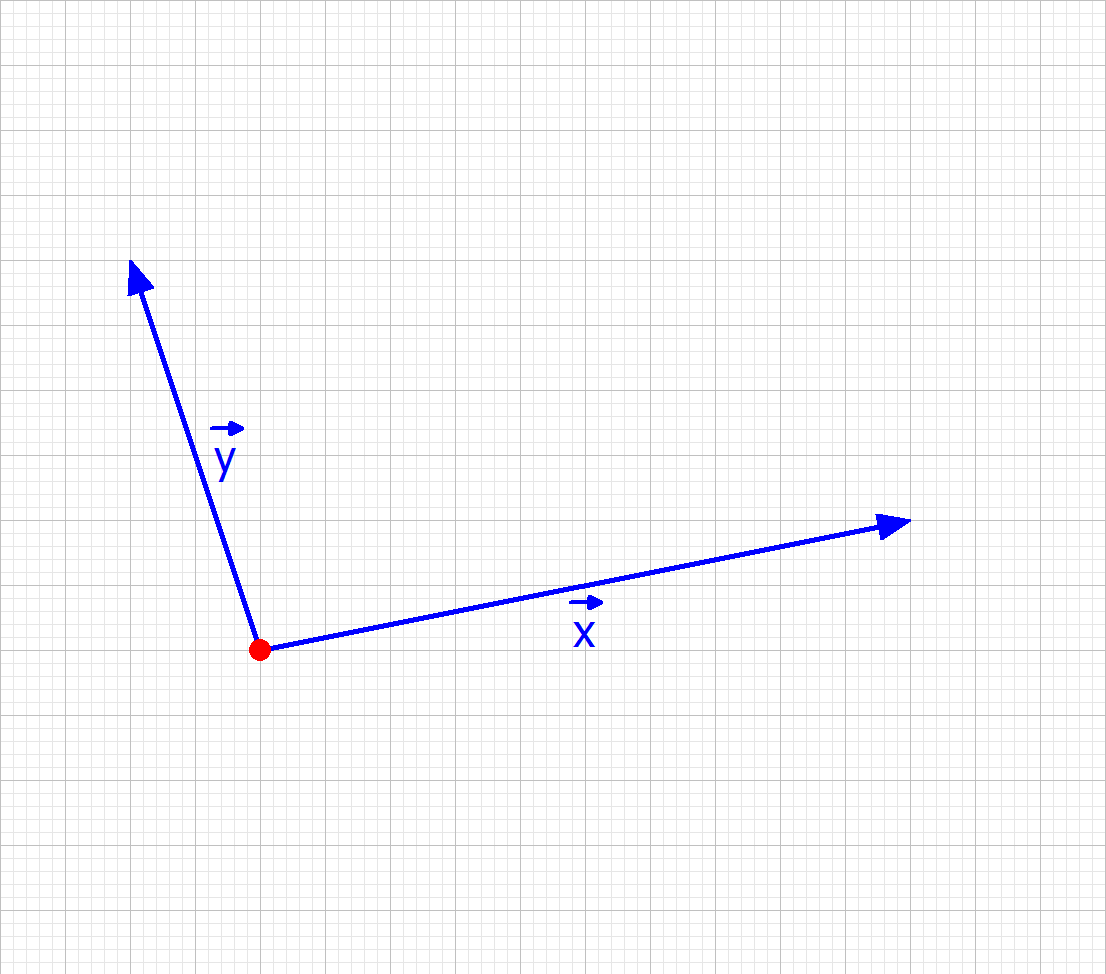
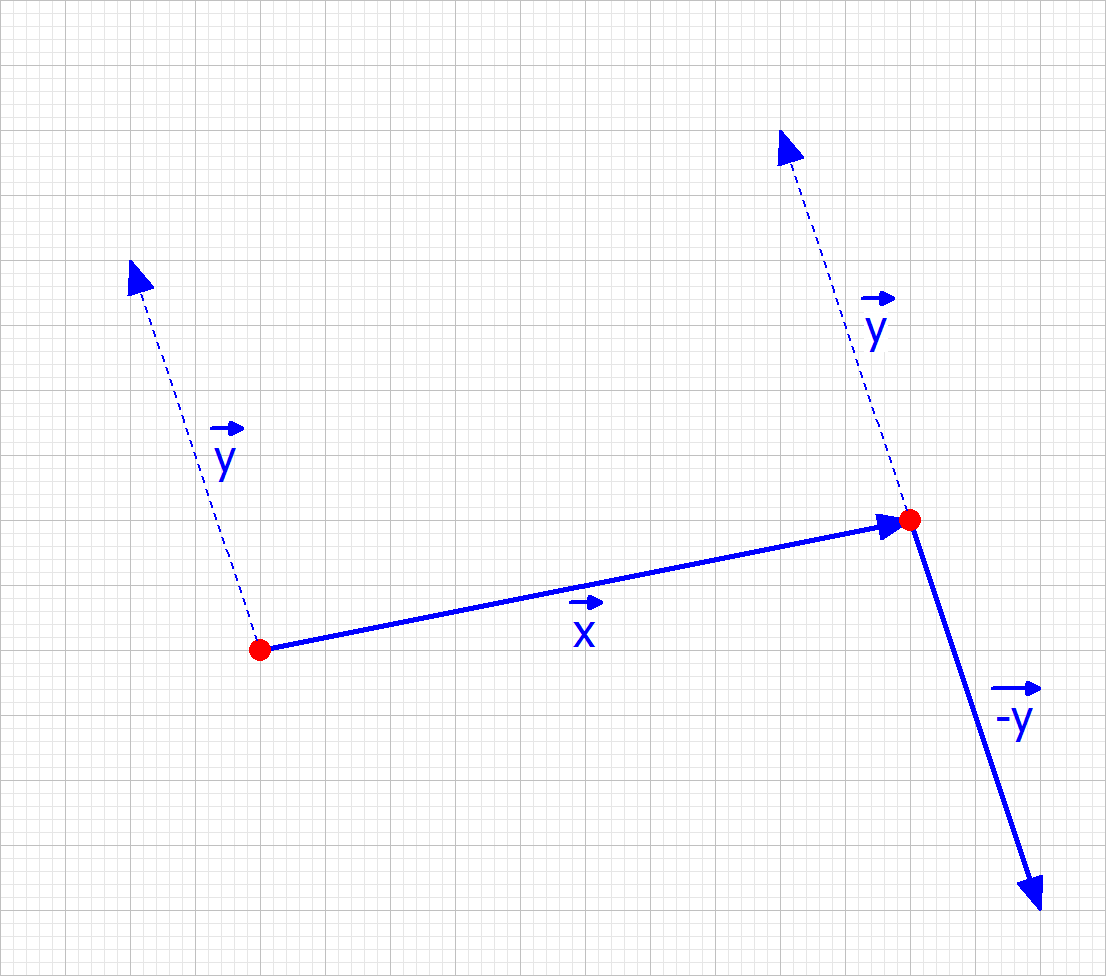
Die folgenden Bilder zeigen, wie zwei Vektoren geometrisch addiert werden. Dazu wird einer der beiden Vektoren parallel verschoben in den Endpunkt des anderen Vektors. Die Verbindung von Anfangspunkt des ersten Vektors zum Endpunkt des zweiten Vektors ist der resultirende Vektor der Vektoraddition.

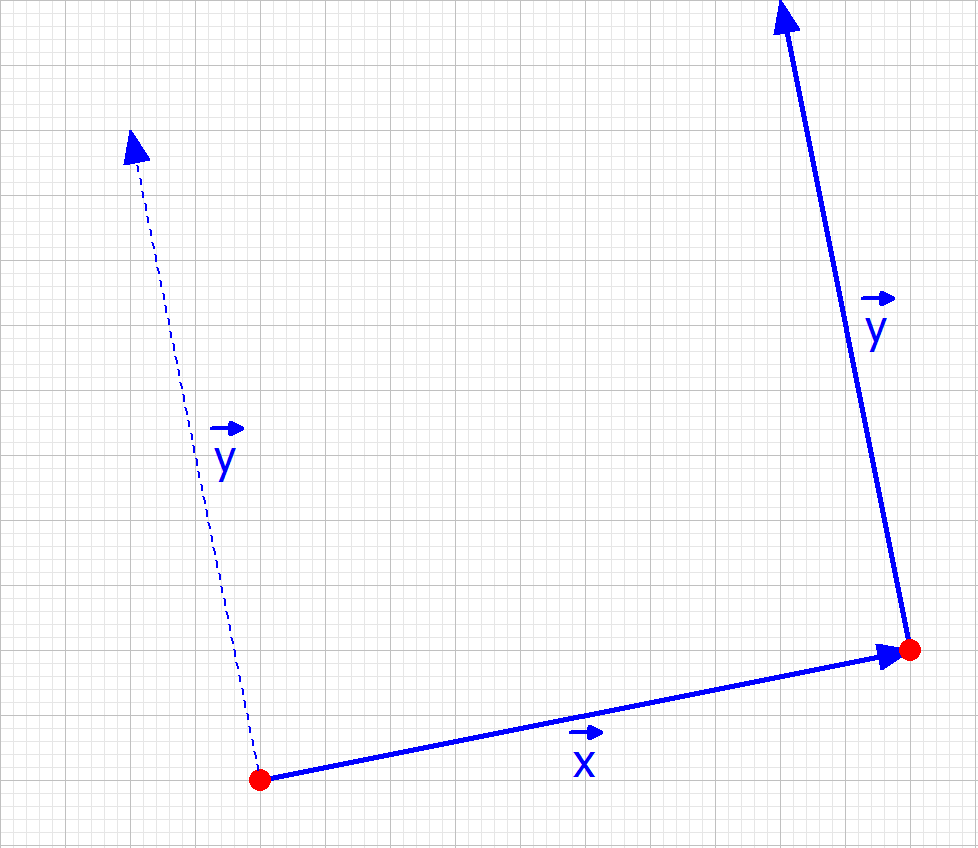
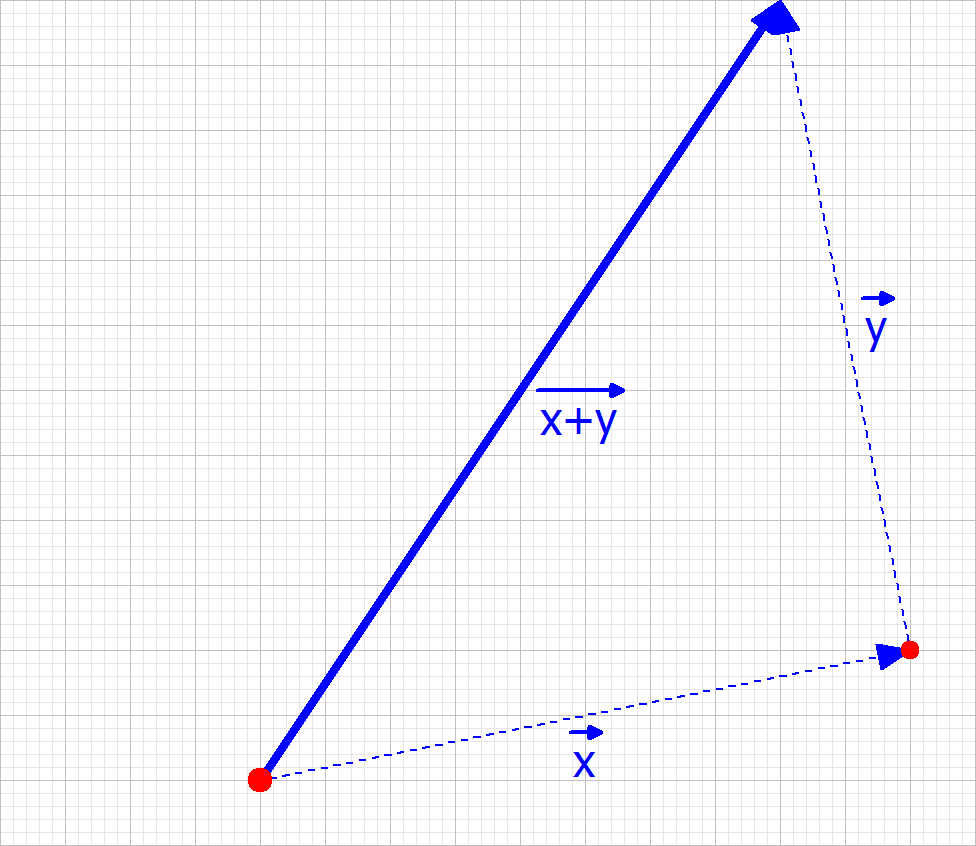
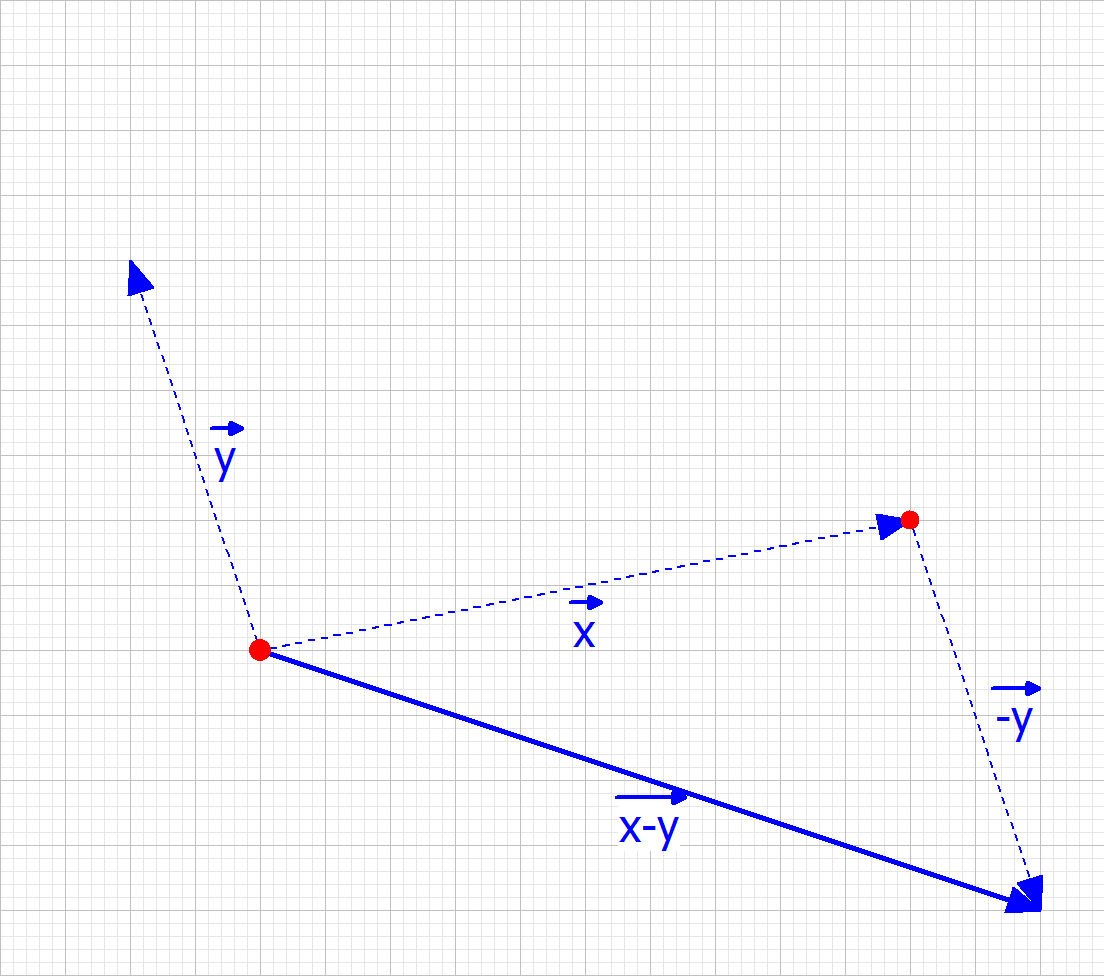
Die Subtraktion verläuft analog zur Addition. Der einzige Unterschied ist, dass der Vektor mit dem negativen Vorzeichen in der Richtung gespiegelt werden muss. Die Verbindung von Anfangspunkt des ersten Vektors zum Endpunkt des zweiten gespiegelten Vektors ist der resultirende Vektor der Vektorsubtraktion.